Contents
In ASG’s universe interplanetary and interstellar distances are not an issue thanks to the hyperspace field that lets ships travel instantaneously between pairs of related jump-points. However orbital mechanics rule in all other flight phases and in effect “DeltaV” is the primary metric to evaluate trips and ship endurance.

The game takes place in the “Quadrans” galaxy, which counts around 14000 stars in 6700 stellar systems in a disk about 12,000 ly in diameter. Its celestial objects are procedurally generated according to a “set of rules” to produce coherent results. Typically orbits must be stable, binary (or higher) stellar systems are common, the radiation from nearby stars is integrated to determine the surface temperatures of planets (and the possibility of liquid water), a giant may migrate toward its star and become a “hot Jupiter”, it may prevent a terrestrial planet from forming and thus generate an asteroid belt instead…
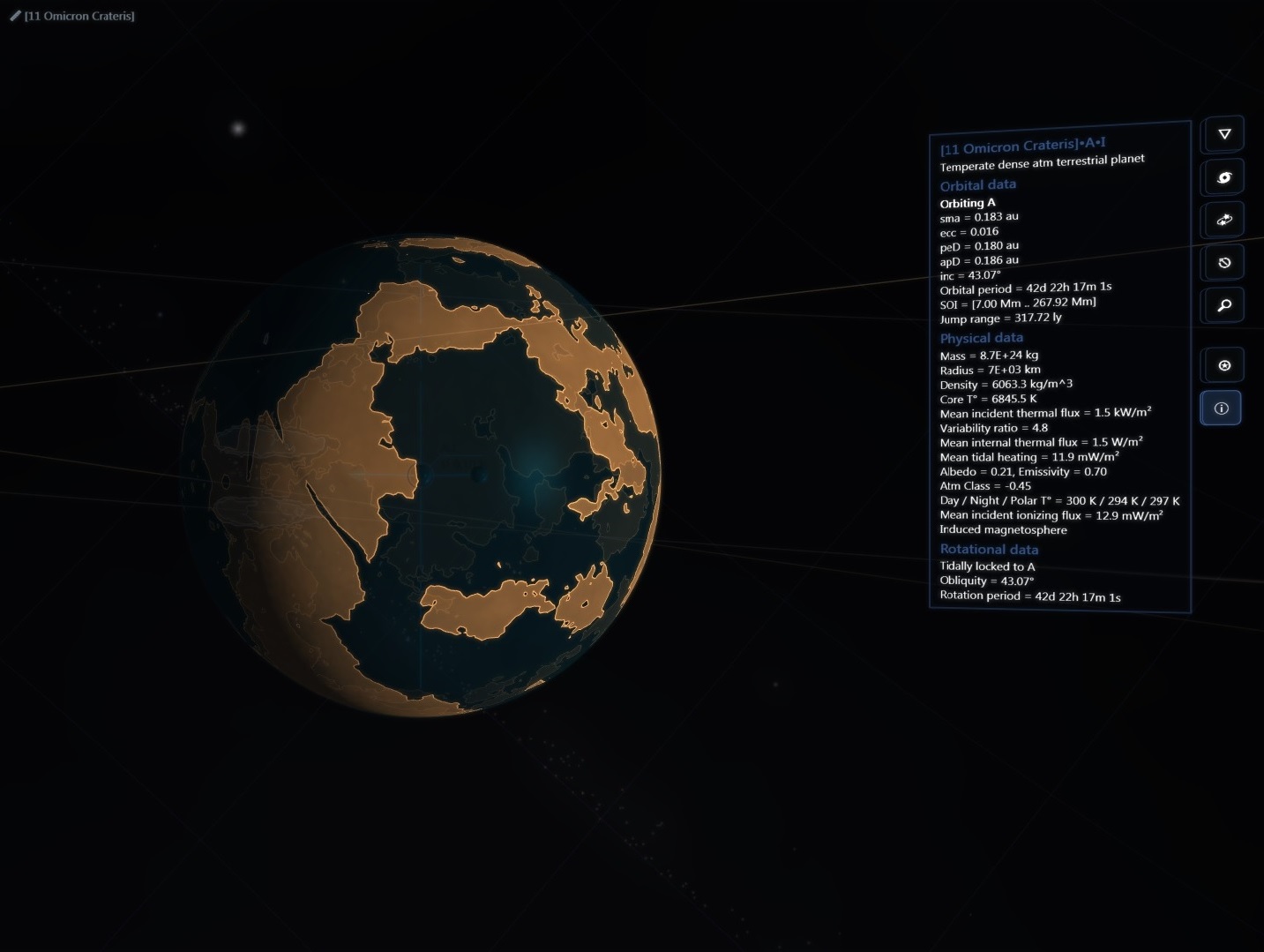

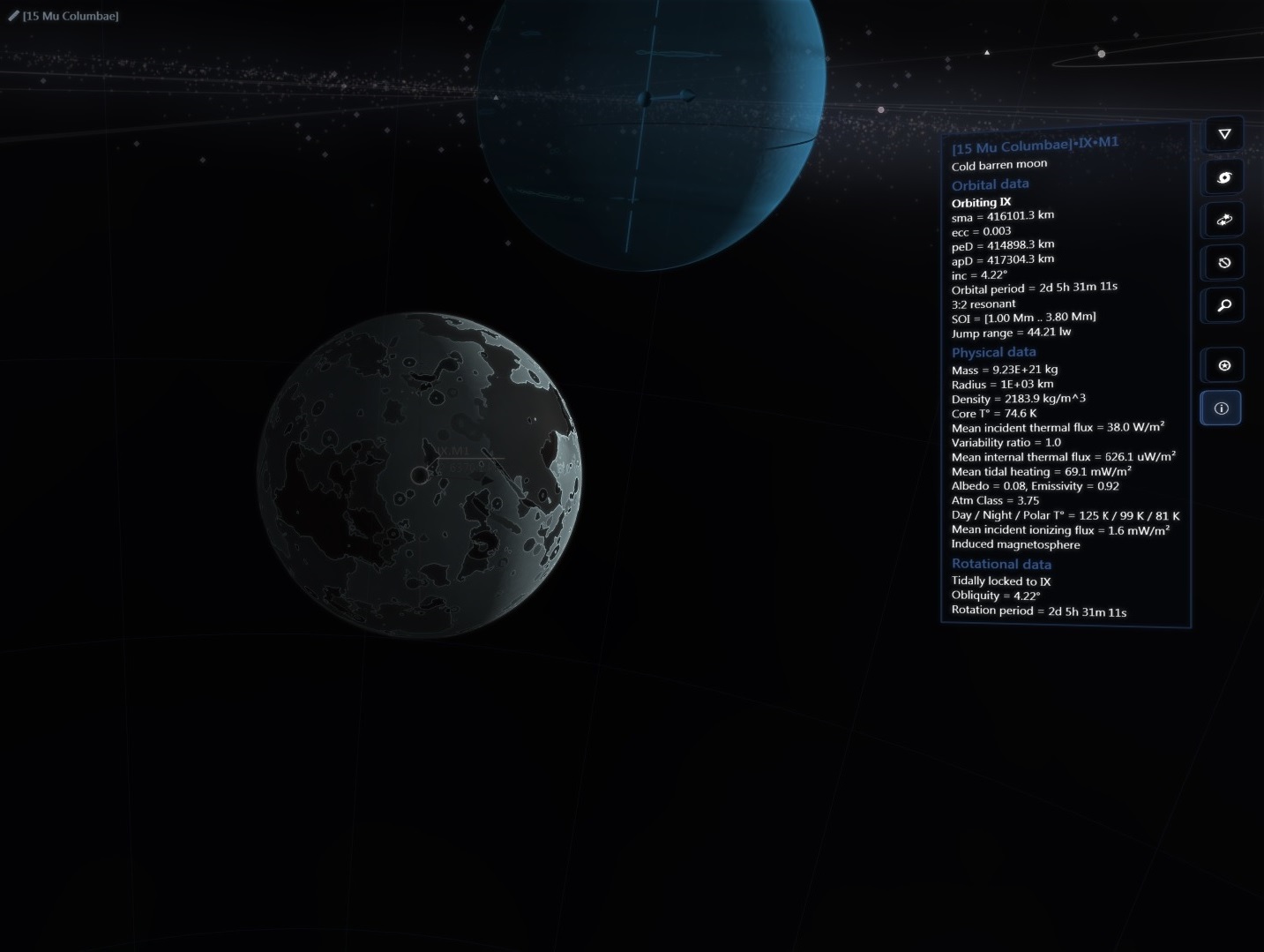
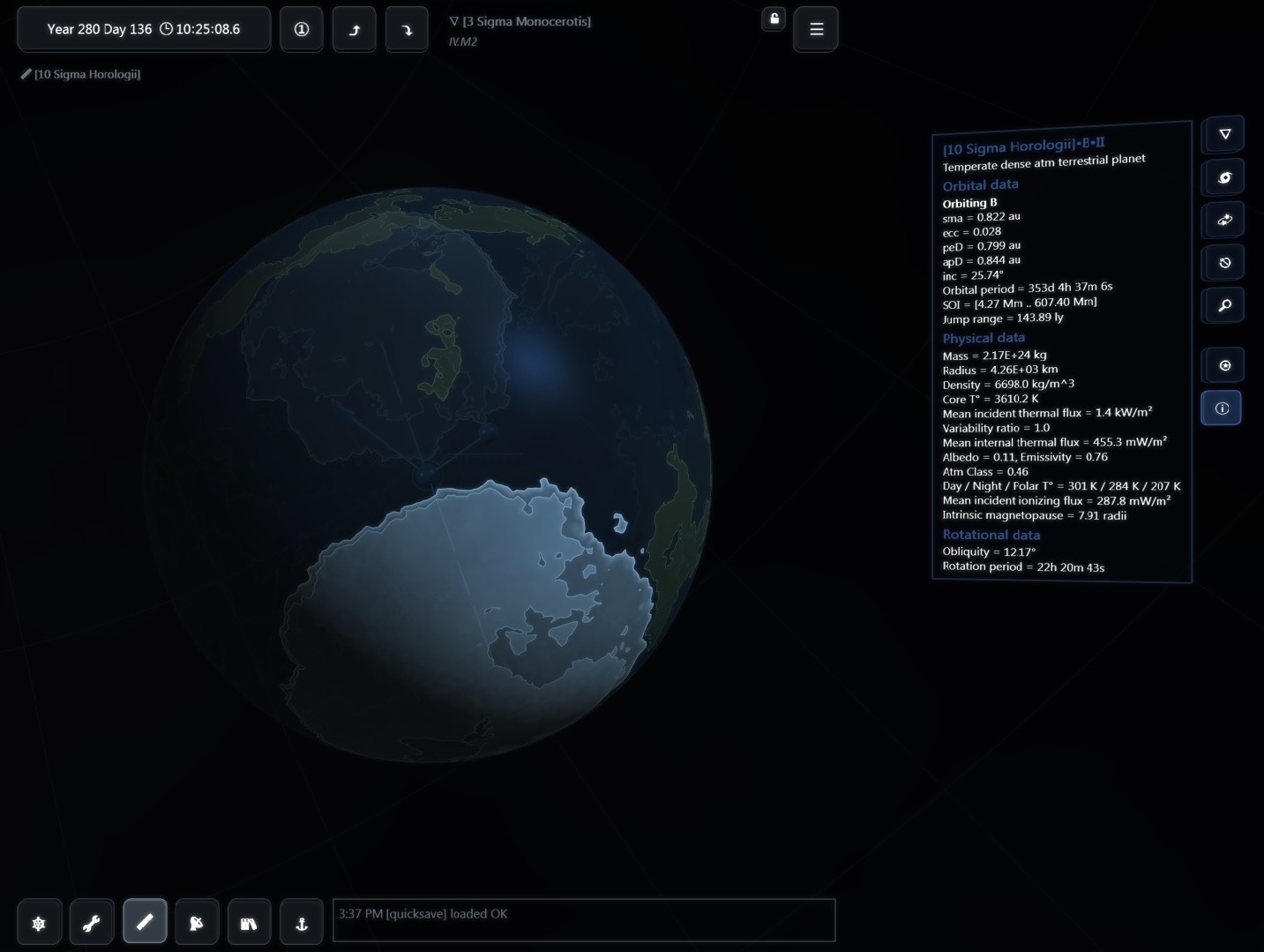
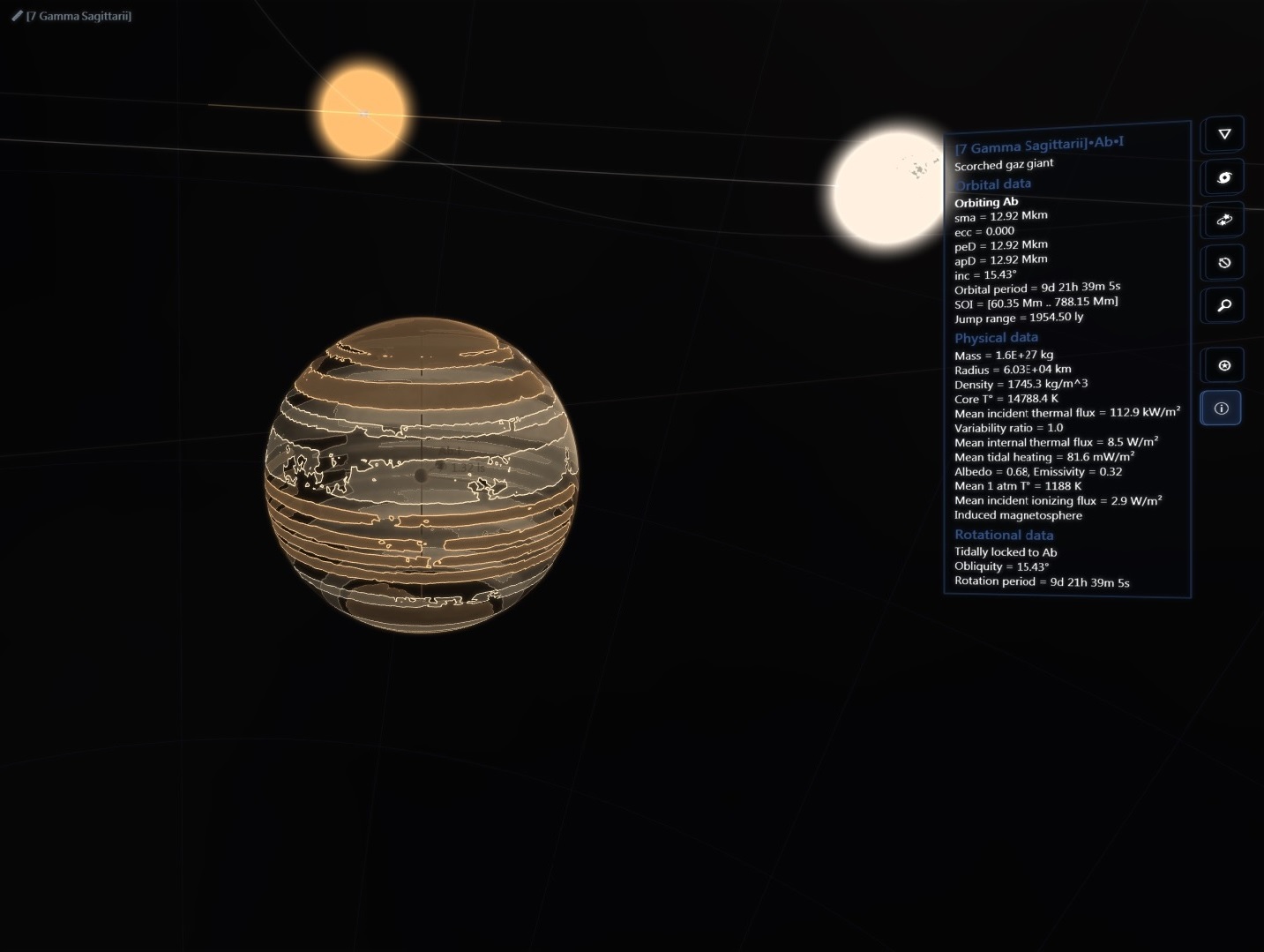
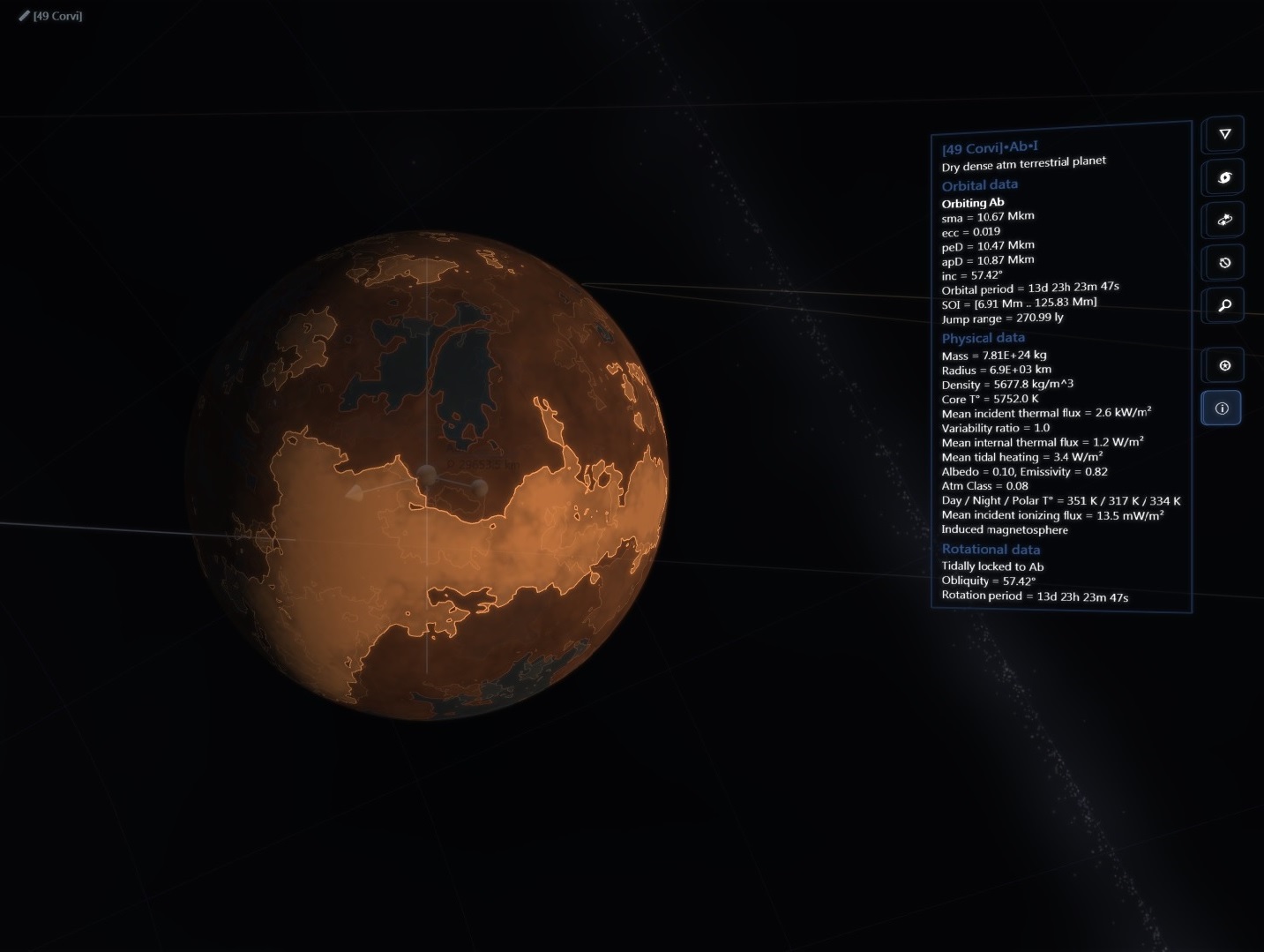
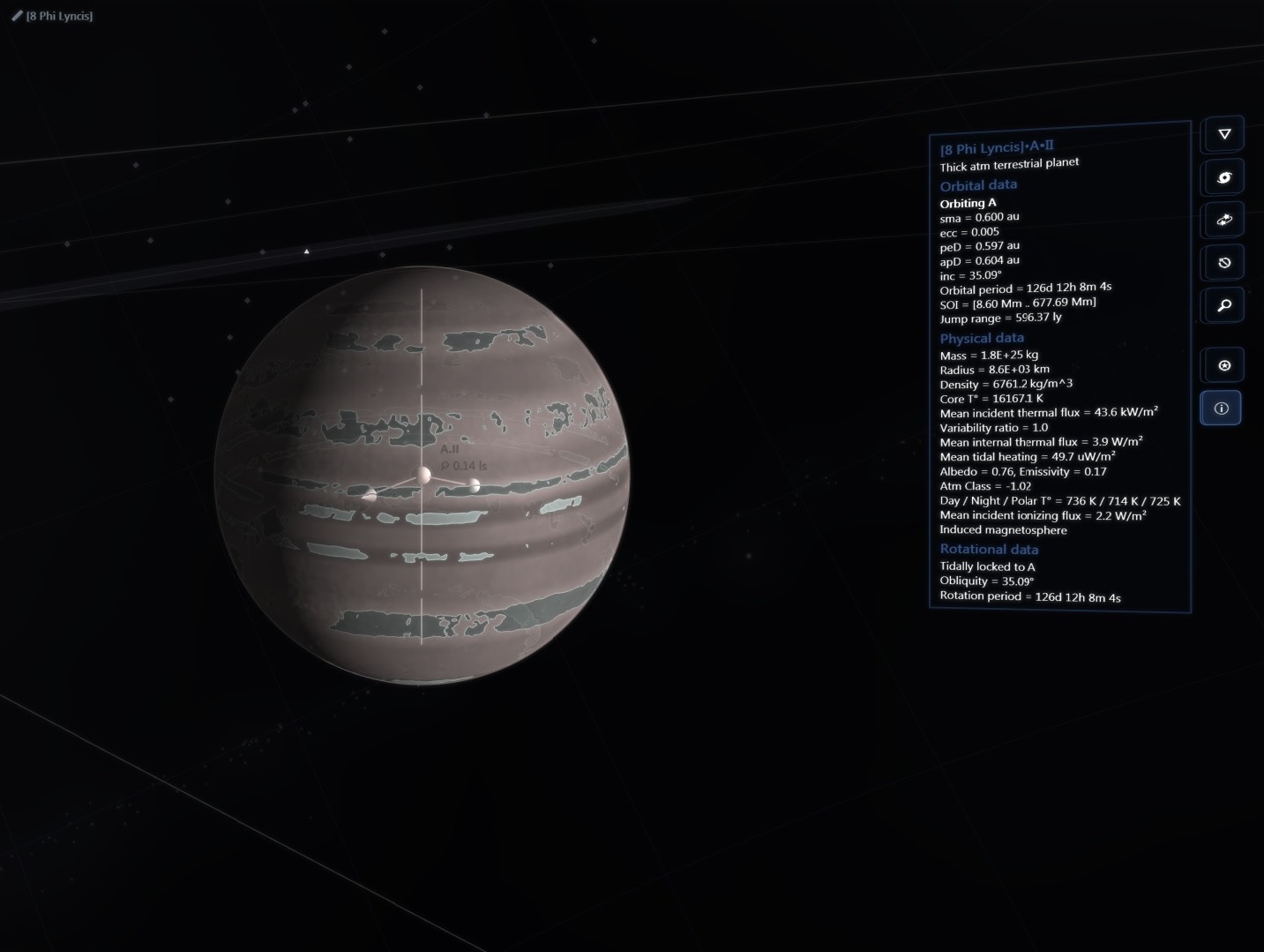
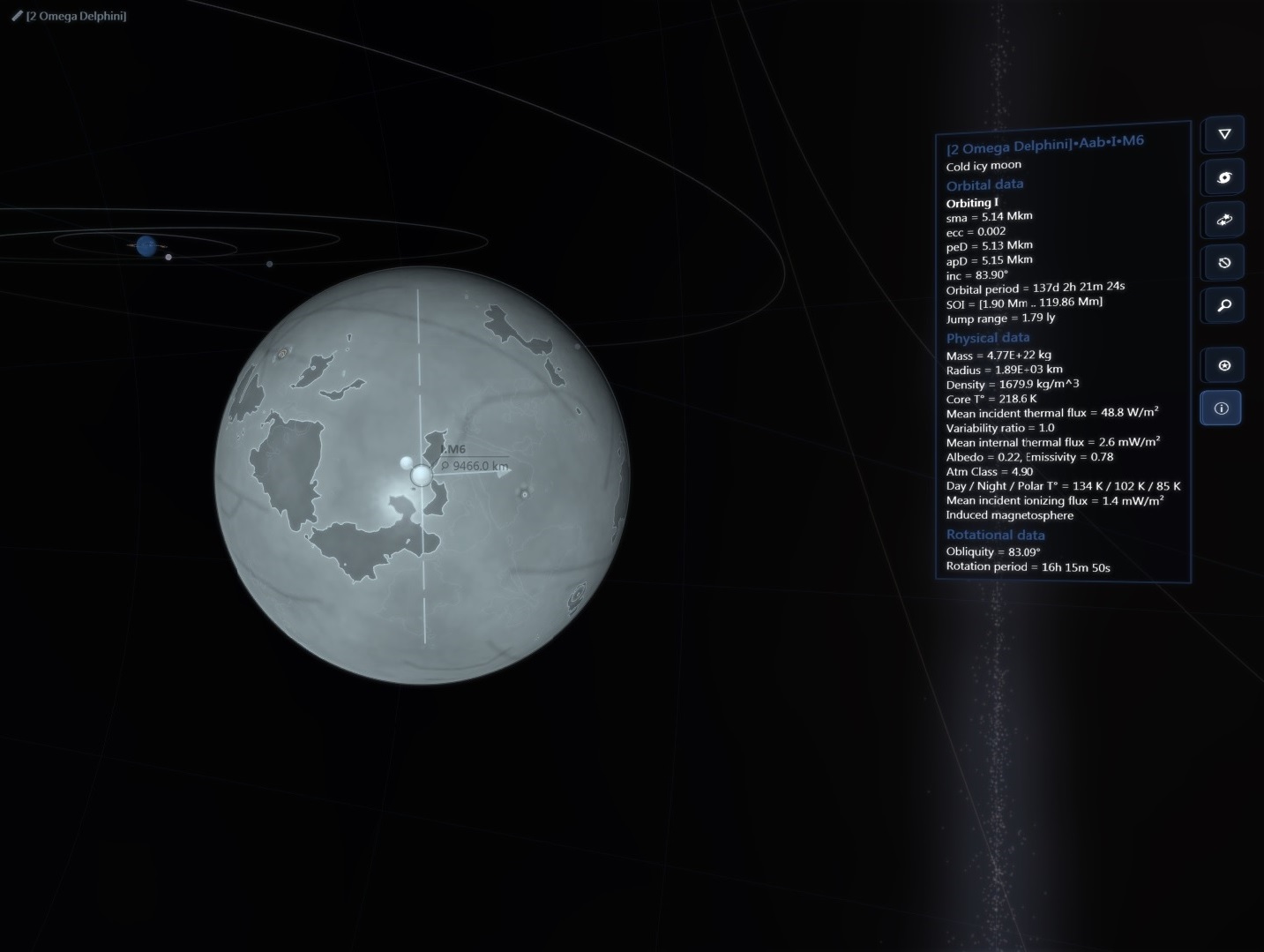
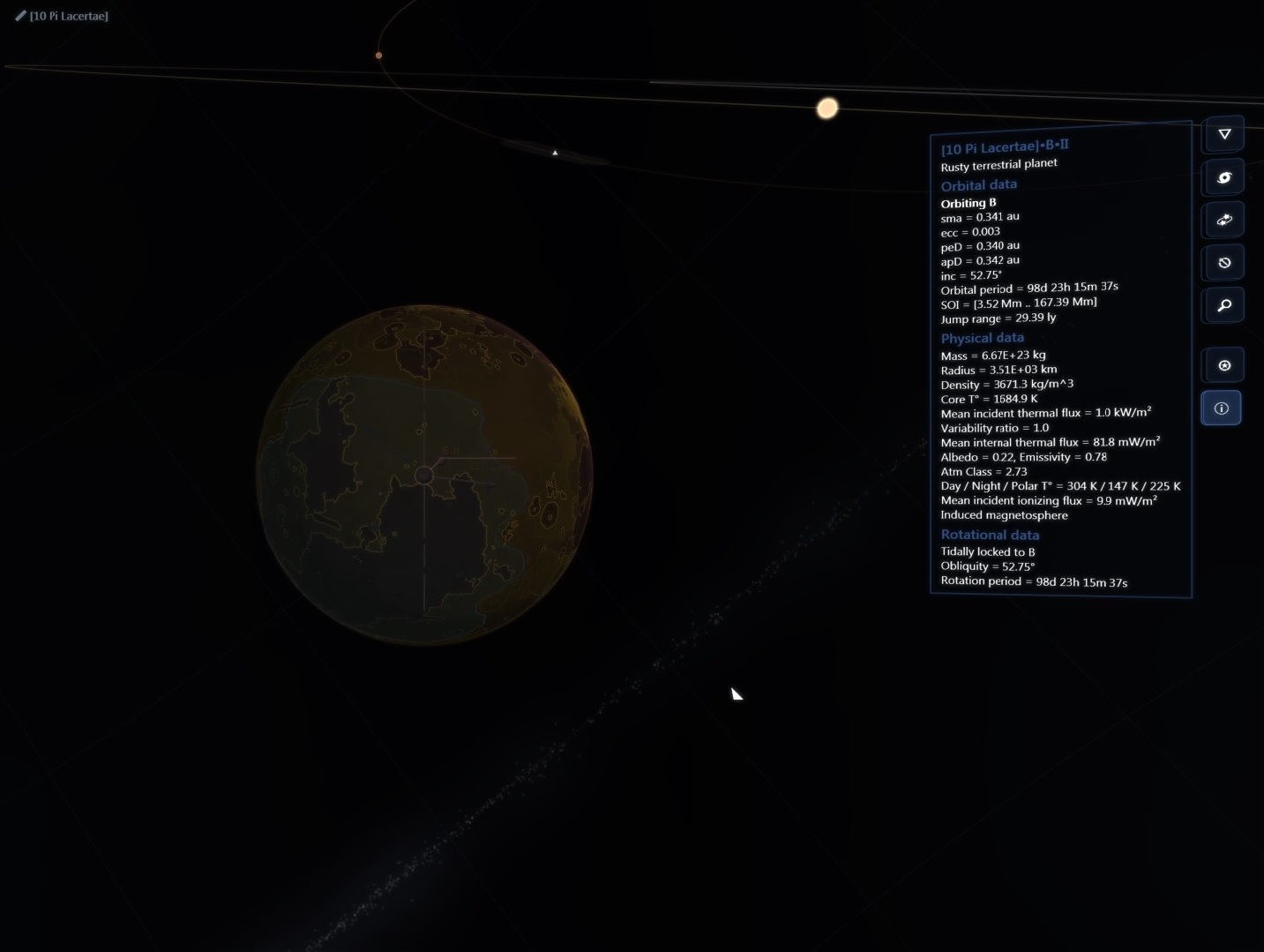
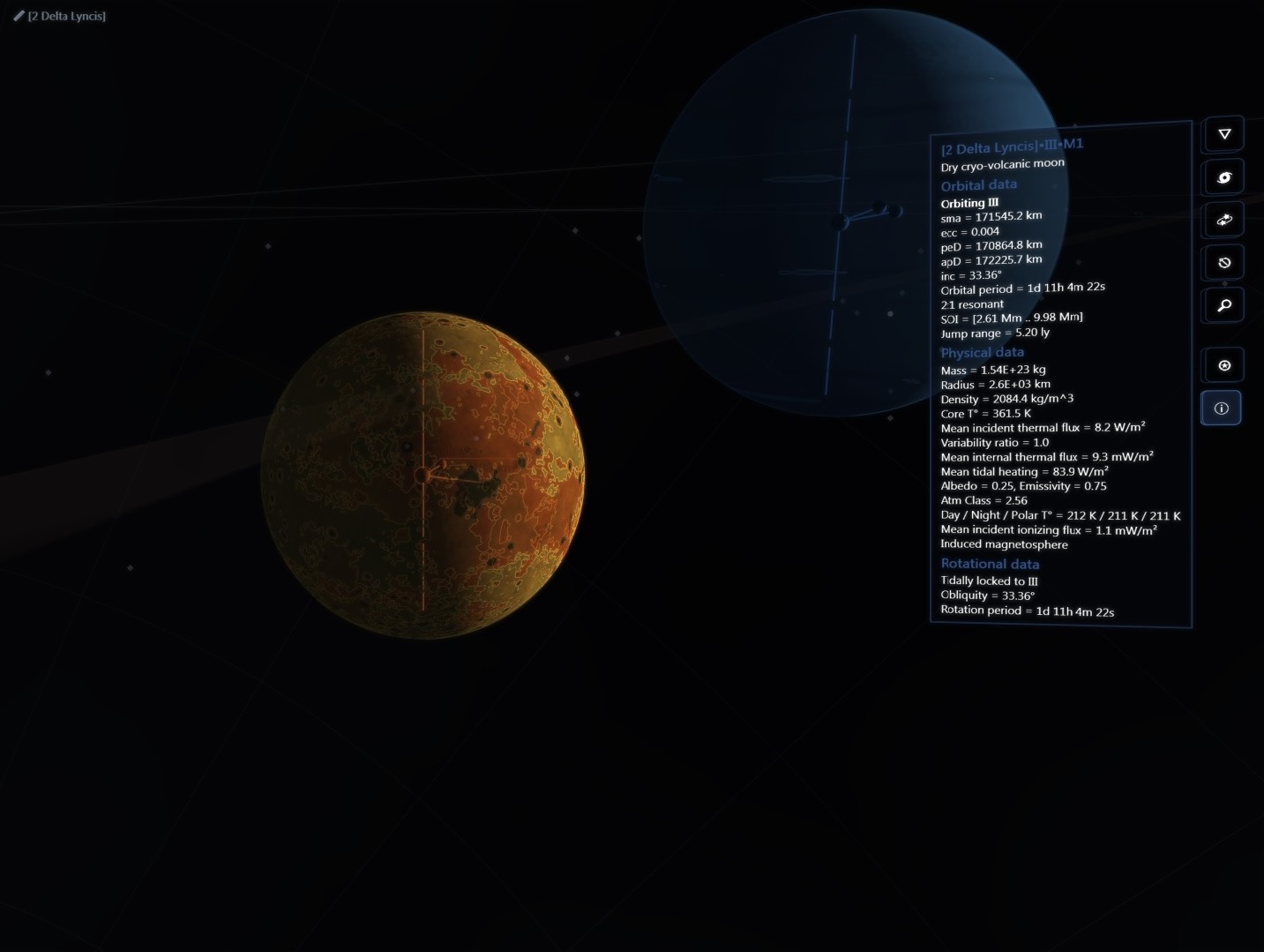
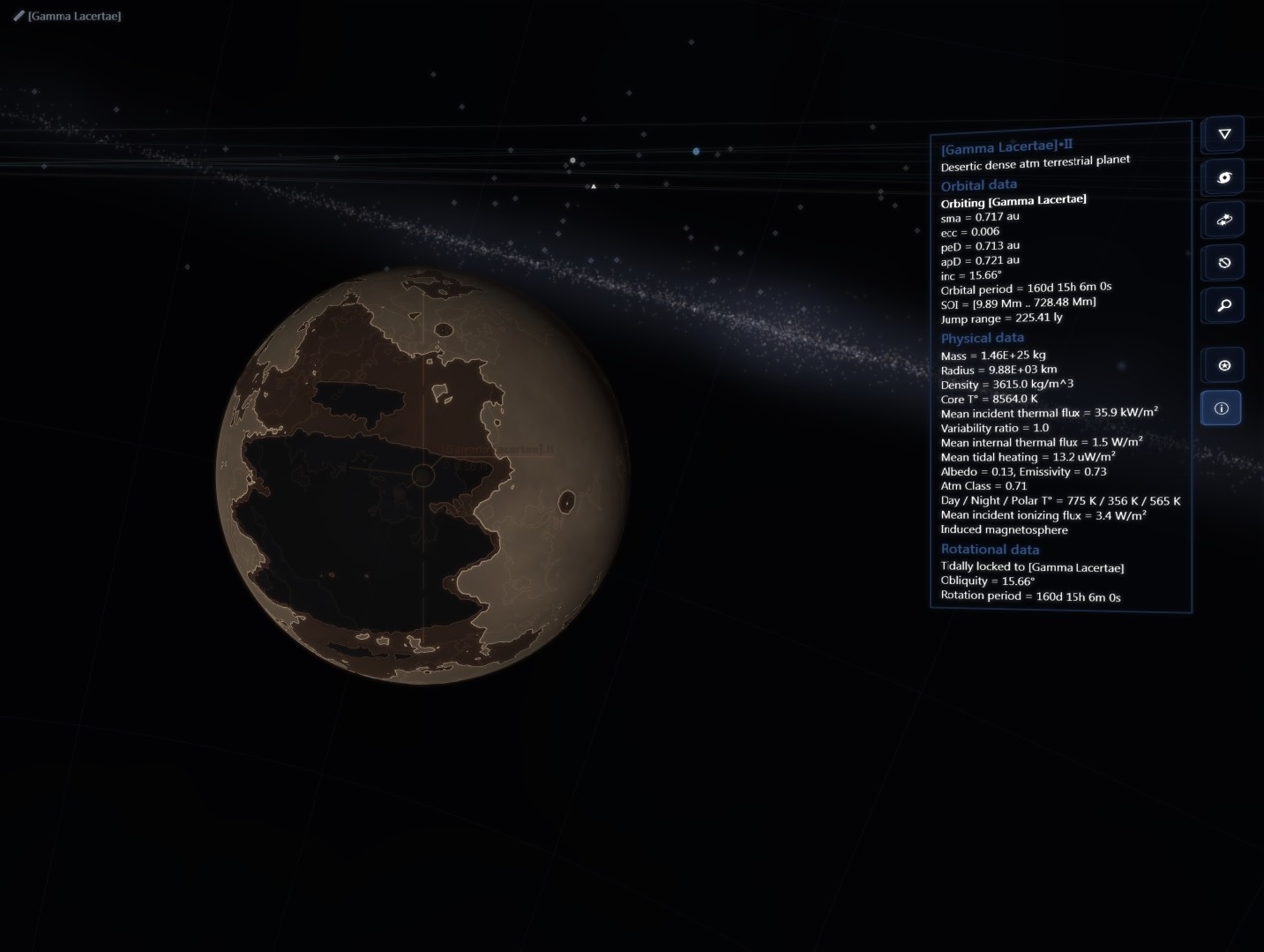
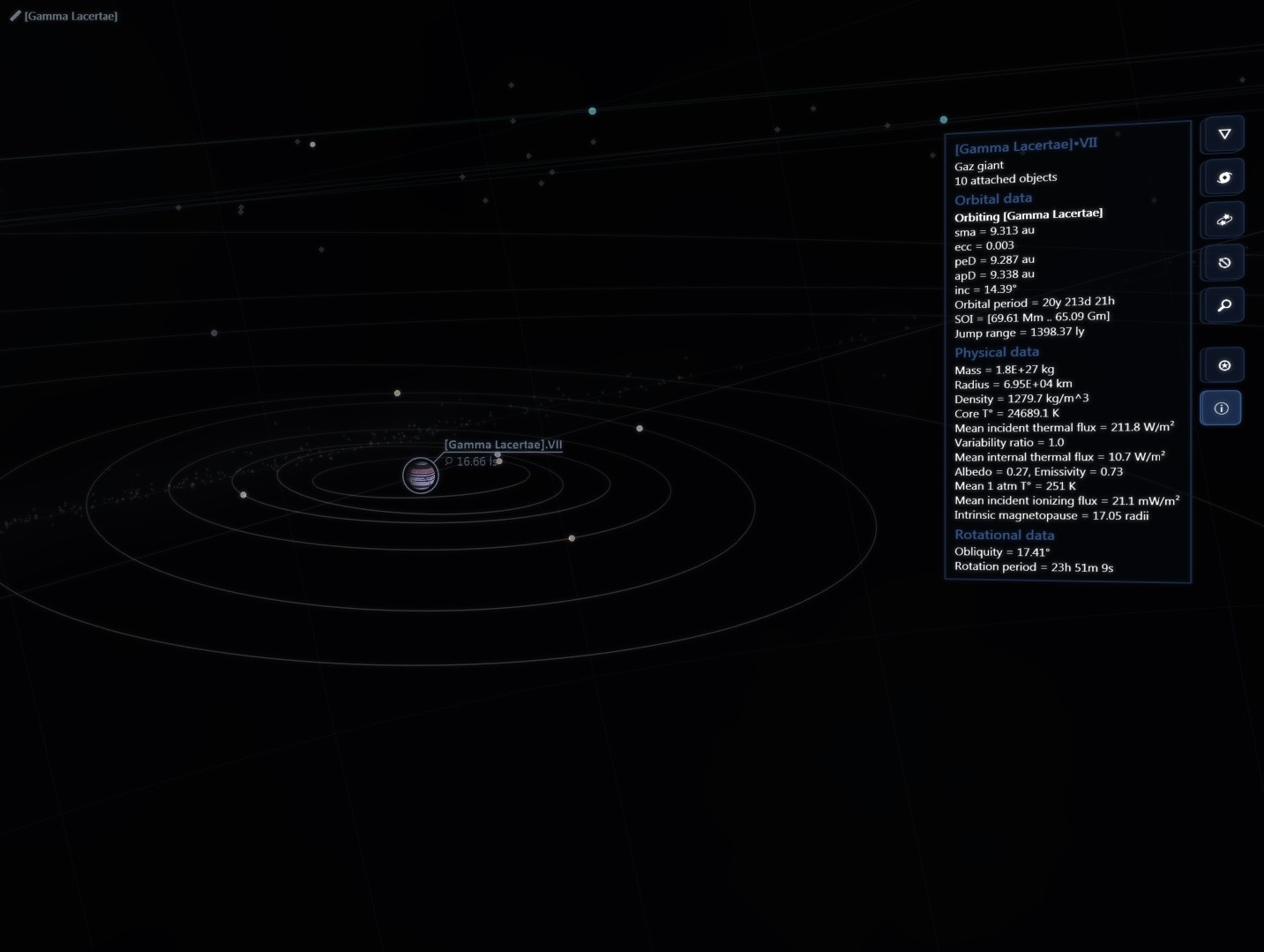
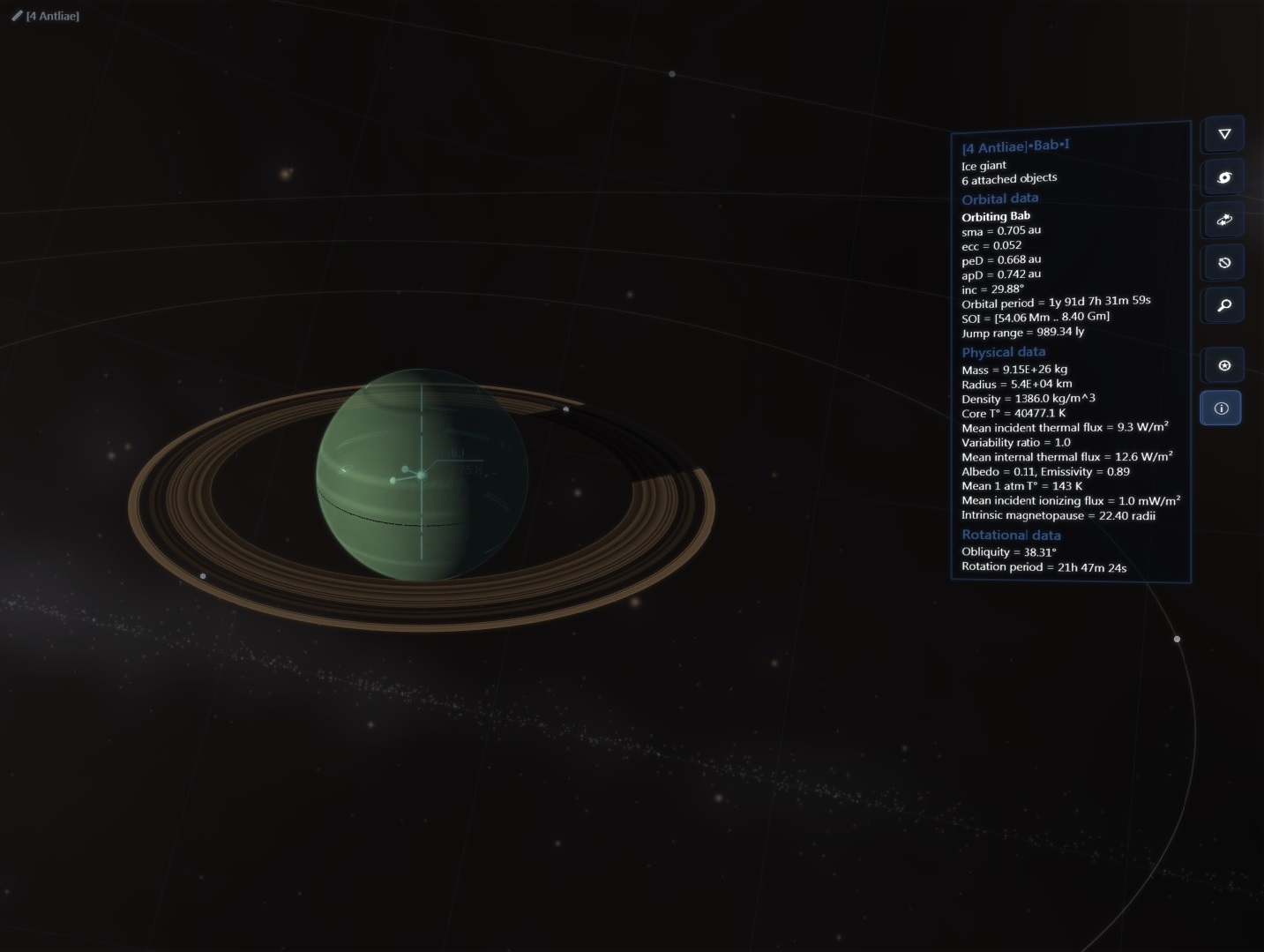
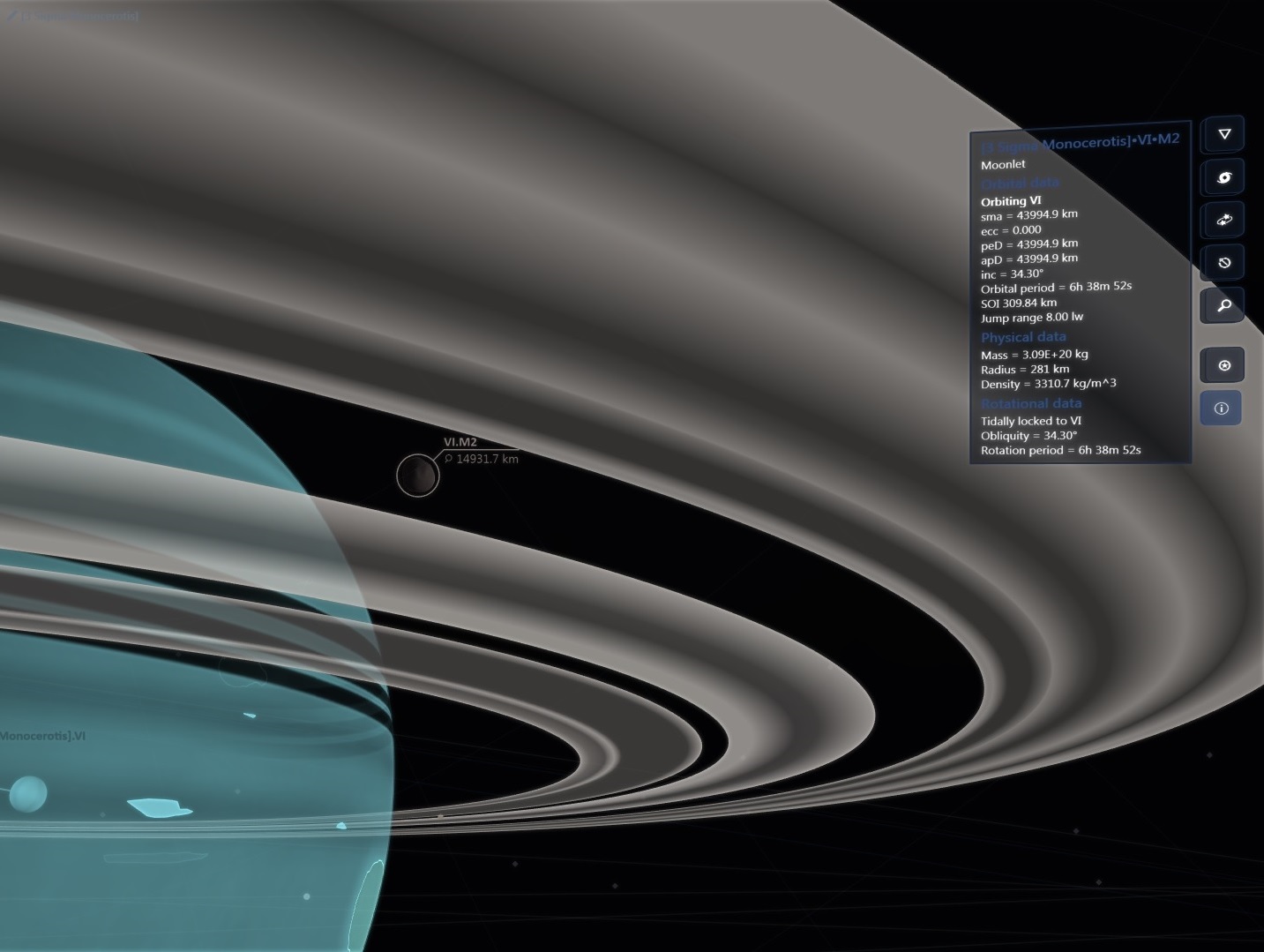
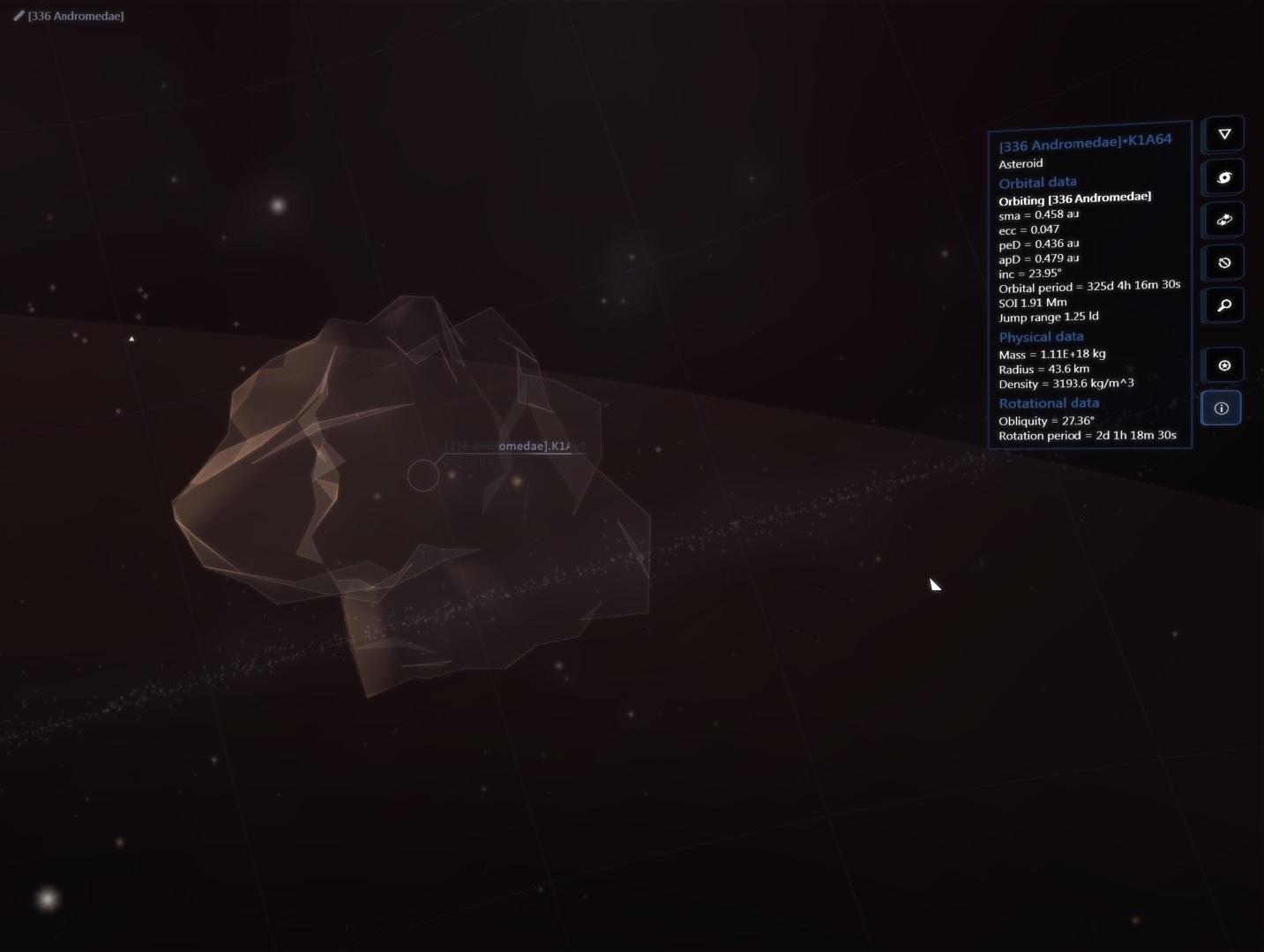
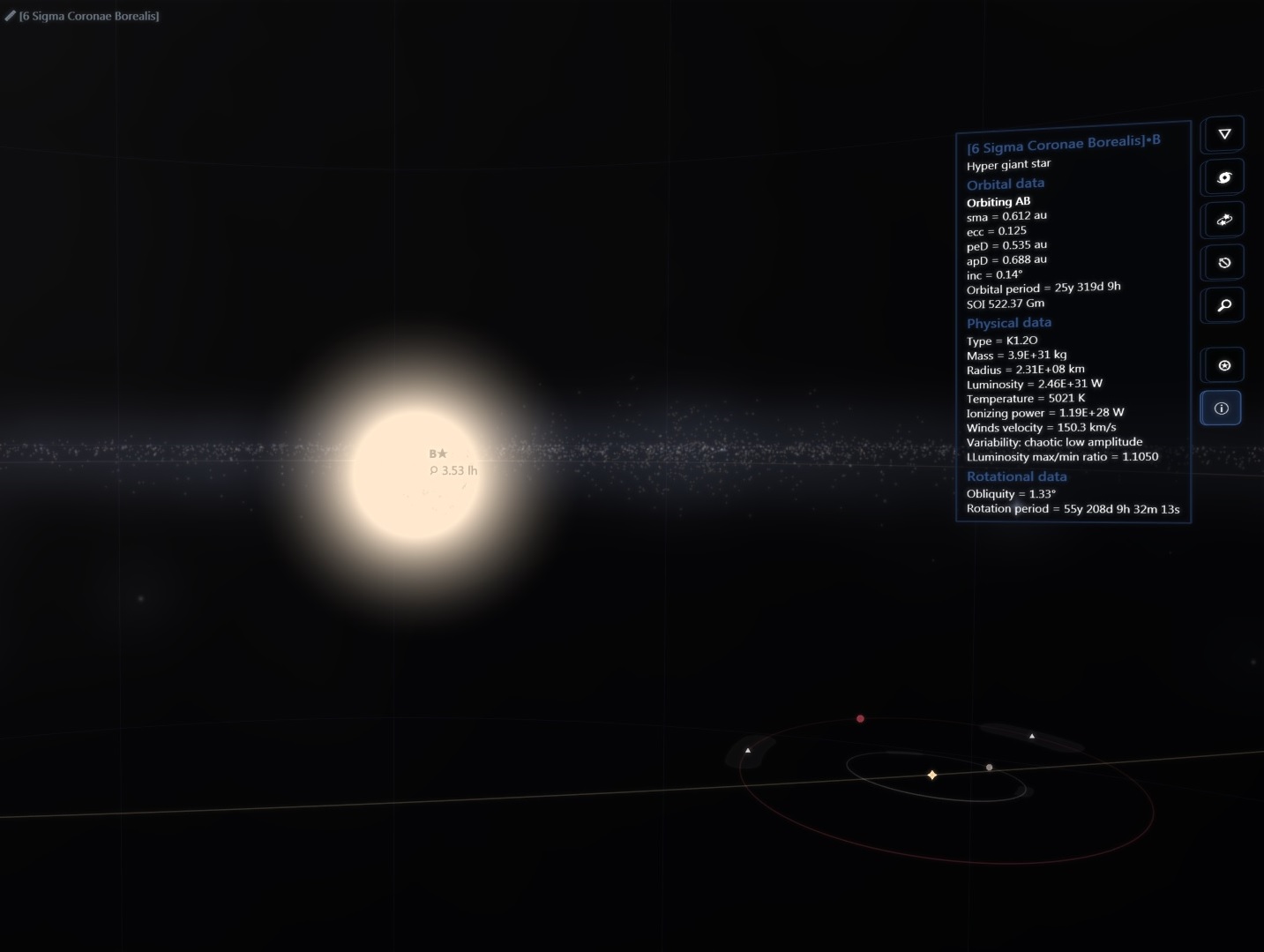
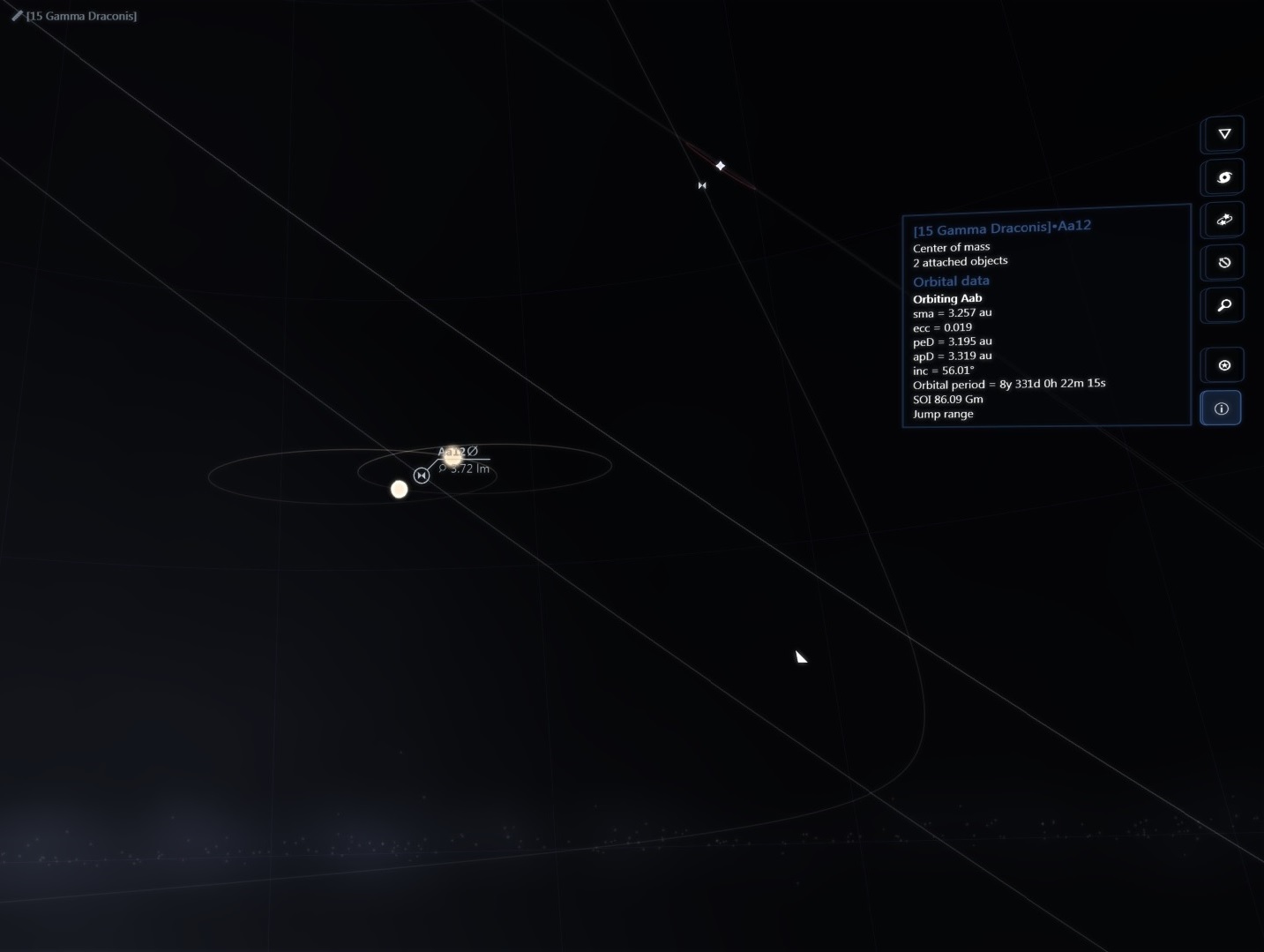
There are about 200 billion stars across 150,000 ly in our galaxy but then again the real universe has lots of RAM!
DeltaV (ΔV) matters more than light years
We are used to evaluate journeys in term of distances but this is not a good metric for space travel. In ASG orbital mechanics do apply and so when orbiting and if submitted to gravity only the conservation of mechanical energy lets you run forever without any effort. Meanwhile you may be covering tremendous distances but are not actually going anywhere.
To adjust their course spaceships apply thrust. Thrust is a force that generates an acceleration (Newton’s second law of motion). Over time acceleration induces a change of velocity called “ΔV = Delta Vee”. Thus at the end of the burn the ship is close to its initial position but now exhibits a different velocity: its orbit has changed. This is demonstrated in the little video below using your ship’s flight planner:
The added maneuver produces 1.20 km/s of ΔV over a 6 minute burn at constant 700 kN thrust, expelling 3.17 tons of propellant mass (H2) in the process.
The Spaceships section explains why the remaining on-board propellant mass (the “fuel” expelled by the ship’s engines) is not a convenient measure of the ship’s endurance either. As a result ΔV is the primary metric used by your on-board avionics.
Jump mechanics
Despite centuries of efforts no consistent theory explaining the hyperspace field has been established yet. However it is believed to be consubstantial with the curvature of space time and the vacuum energy. In classical terms and compared to gravity it exhibits a similar radial symmetry but with different dependencies on mass and distance.
Its main property is to connect pairs of specific locations around distant celestial bodies and corresponding to matching field values. These locations are commonly referred to as jump-points.
In effect jump drives create an anomaly region of “quantum hyper-coherence”, a process called jump-space polarization. The region is spherical and centered on the jump drive, and state of the art devices require several hours to expand it so the whole ship is safely contained.
Jump-point pairs exhibit a natural oscillation that is related to their relative motion and called the “hyper-doppler” effect. Correspondingly the anomaly must be excited at a matching phase and frequency and the operation is referred to as jump-space modulation. A jump is successful if the energy release occurs while the jump-point is enclosed. As a result the extension of the anomaly region sets the required navigation accuracy. Again the physical process is not really understood but it is generally accepted that the event probably corresponds to “the universe taking a shortcut” to a lower energy state.
Due to the shape of the hyperspace field mechanical energy is not conserved during a jump. However momentum is and consequently ships retain their velocity. In the respective parent reference frames, the exit velocity thus equals the departure velocity plus the relative motion between the bodies (jump ΔV below). Flight planning routines takes these rules into account to discard dangerous solutions leading to unavoidable collisions. More generally they optimize the approaches to jump-points so as to minimize the overall ΔV cost.
Regardless of actually existing hyperspace connections, the maximum jump distance for a given celestial body is set by its mass and the minimum safe approach altitude. On the other hand the minimum jump distance is related to its sphere of influence. Regions where the space time curvature is very complex due to the combined gravity of many surrounding bodies generate evanescent and unreliable jump-points that are automatically discarded by navigation routines.
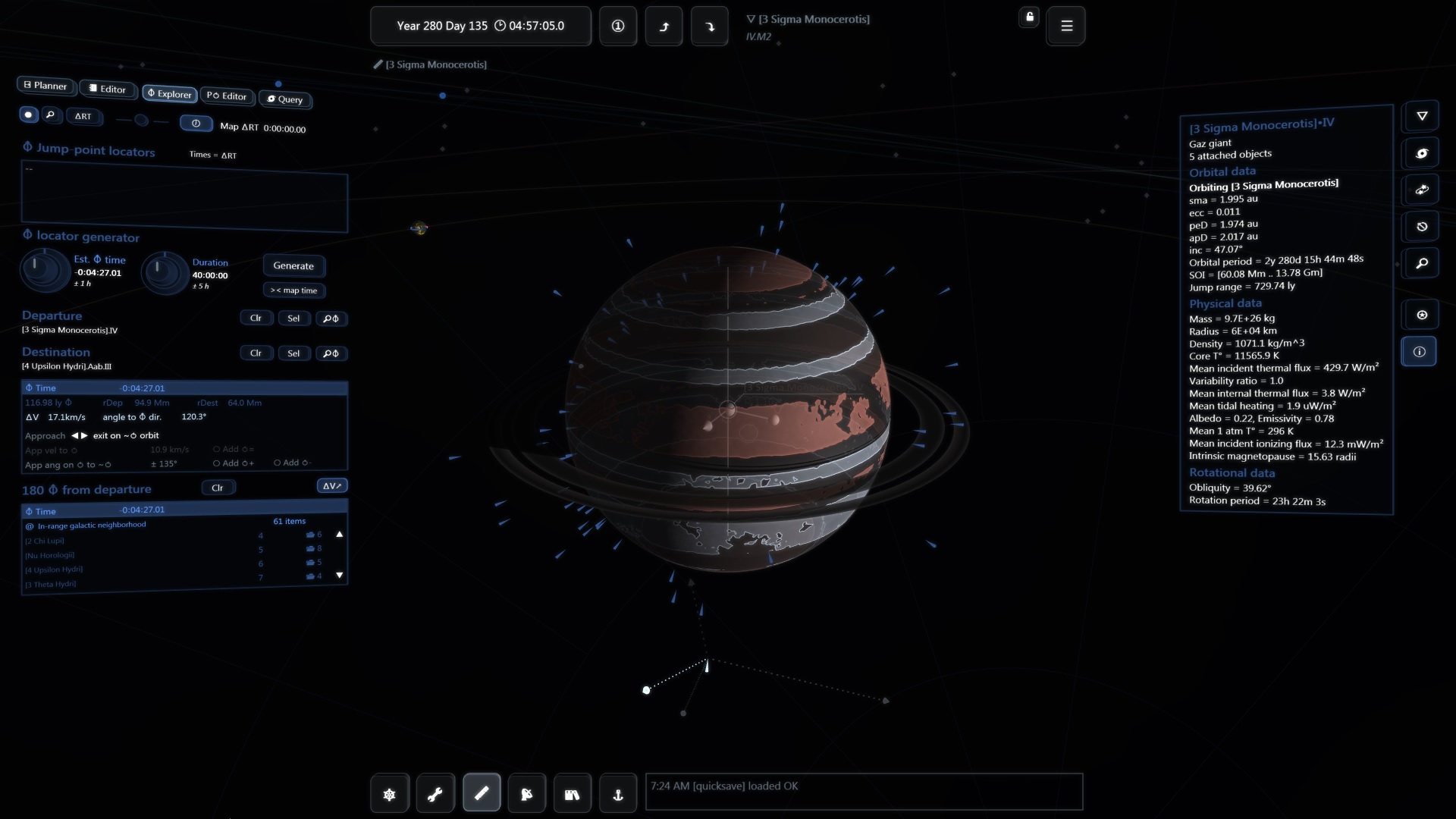
ΔV matters for jumps too
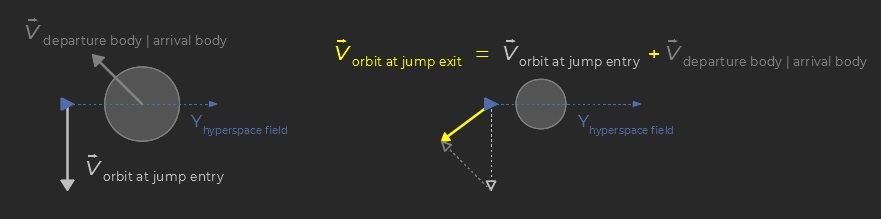
Flying a jump: