Contents
Ships in the Quadrans galaxy
After nearly three centuries of space travel, technology may continue to improve but the specifications for the different classes of spaceships are now well defined.
Typically cargo vessels and passenger liners always use the available shipping lane of least ΔV (“Delta V”) cost at their time of departure and wait for a more favorable launch window if need be. In effect they hop from one refueling station to the next and will rarely perform hard orbital maneuvers. As a result they are optimized for moderate accelerations and a nominal ΔV budget around 80 km/s.
Quite differently military ships must be able to swiftly alter their course to intercept a target and simultaneously be capable of return trips without refueling. Their ΔV capability is generally around 100 km/s and a₀ > 1.5 m/s² (see below). While it may not seem to be particularly impressive, that performance level is typically achieved while carrying tens of tons of military payload and armor.
Private luxury vessels constitute the third main class. While generally lighter than military ships they exhibit similar ΔV and acceleration capabilities. Most of them are perfectly harmless, but they may represent a significant threat once their lush interior is removed and the spared mass reused to fit weapons instead. The method is typically favored by organizations lacking the resources to afford actual warships.
Finally tankers are essentially cargo ships with oversized LH2 tanks. They can also double as utility vessels and also be used to reach specific locations thanks to their large ΔV budget.
A useful figure of merit to help compare designs is the Initial Acceleration for 100 km/s or “a₀, a – zero” (the associated ΔV is always 100 km/s if not specified). It represents the acceleration the vessel can deliver with full tanks while being able to accumulate 100 km/s of ΔV if continuing to burn at the initial thrust level.

The thrust [N] from a rocket engine is given by:
The specific impulse [s] is simply related to the exhaust velocity:
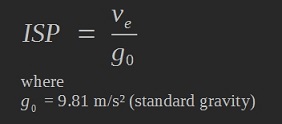
The mechanical power of the expelled propellant mass is given by the equation below. It is generally generated by a fusion reactor with conversion from thermal to mechanical work by a magnetic nozzle. The losses (η < 1) are due to numerous contributors (primarily reactor servicing equipment consumption, unconfined plasma radiation, non-ideal nozzle conversion)
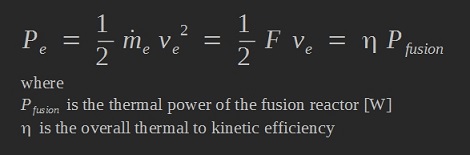
The ΔV budget is given by Tsiolkovsky’s rocket equation:
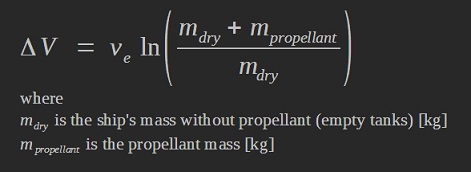
The a0 indicator [m/s²] is expressed as follows:

Note: the efficiency of the conversion from the fusion thermal power to the kinetic power of the exhaust flow generally depends on the associated thrust. This is due to the fact that the effective expansion ratio of the magnetic nozzle decreases at higher thrust levels.
Given a dry mass and available power a0 can be used to determine the optimal propellant mass in terms of available acceleration. Below is a plot corresponding to the CSN F9 class:
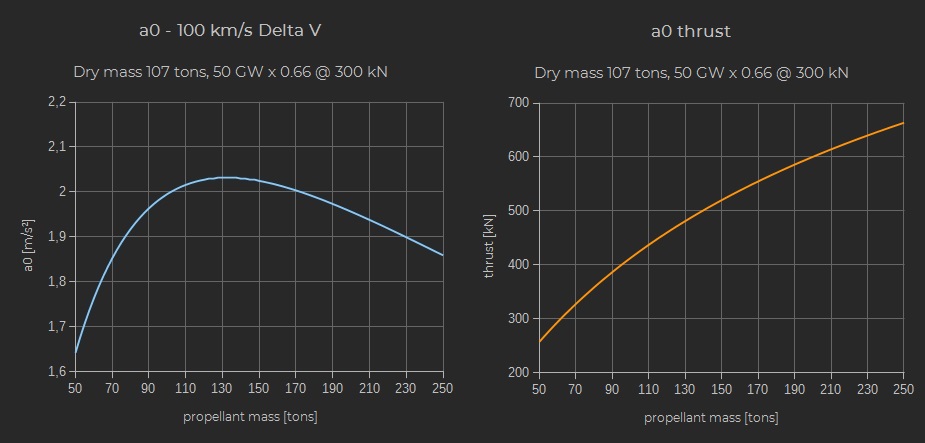
Recalling that the product of the thrust by the exhaust velocity (or ISP) is a constant proportional to the available power the plot can be interpreted as such:
- With insufficient propellant the ISP must be very high to reach the ΔV budget. This imposes a low thrust and consequently a low acceleration despite the reduced total mass.
- Beyond the optimal point the thrust cannot be augmented as fast as would be required to compensate for the increasing mass, otherwise the ISP would drop too much and the ΔV budget would not be met.
Propulsion system
The best chemical engines in the Alliance exhibit an ISP around 570 s (LH2 – cyclic O4). A ΔV budget of 100 km/s would thus require a mass ratio (total mass over dry mass) around 40 million, obviously unfeasible by many orders of magnitude. Moreover some reasonable assumptions regarding mass and acceleration lead to a required specific power in excess of 100 kW / kg.
Nuclear fusion is the only known technology that can deliver this kind of performance and all newly developed spaceships have been powered by Deuterium + Helium-3 reactors for a long time. Using the latest advancements in carbon-carbon metamaterials and high-power active magnetic plasma confinement it is now possible to build ships in the 50 GW / 100 tons range. The CSN F9 is a typical example of this new generation of military vessels.
D / He-3 reactors deliver their power as a flow of ultra-hot plasma (typically 300 keV ~ 3.5 billion K). At such a high temperature the corresponding mass flow is very small, around 2 g/s at 50 GW. Supposing a perfect expansion of this plasma into a magnetic nozzle yields an exhaust velocity of more than 7000 km/s (ISP 700 k). Nevertheless the corresponding thrust does not exceed 14 kN for an acceleration of less than 0.14 m/s². This does not meet the usual acceleration requirements by a factor 10. Moreover such an engine would deliver 100 km/s of ΔV in more than 200 hours at maximum power, which actually exceeds the life expectancy of existing reactors.
Consequently the fusion plasma is not used directly as propellant. Instead it is mixed with hydrogen in the Exhaust Mass Augmentation (EMA) chamber to produce a larger quantity of lower temperature “exhaust plasma” (typically 80 eV). When expanded in the magnetic nozzle this plasma produces the desired characteristics, i.e. ISPs around 10 ks and thrust levels > 500 kN. This is similar in essence to jet engines whose propulsion is provided by the expanded air flow after heating by the fuel combustion rather than by the combustion products themselves.
Hydrogen is used as propellant because it is the lightest and therefore most effective element for this role. It also happens to be easily extracted from water ice which is widely available in most stellar systems. To minimize the necessary volume it is stored in cryogenic tanks in liquefied form (“LH2”) which corresponds to its state of maximal density.
Mass ratios around 2 are common, that is dry ship mass ∼ LH2 mass. As a result at constant thrust and power 1 ton of hydrogen will deliver roughly twice as much ΔV (and acceleration) with near empty tanks than with full ones. This is why the on-board quantity of hydrogen is only a secondary indicator for a ship’s endurance and ΔV is the preferred metric.
Because of their flight profiles involving multiple burns, staging would not be practical nor economical and all designs are technically single stage rockets (no jettisoning of propulsion hardware, propellant mass carried in internal tanks).
(more information available on the Nuclear Fusion and Main Engine pages)

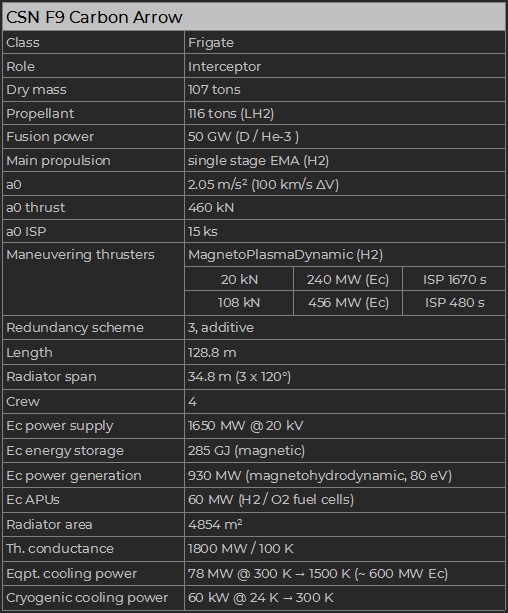
CSN F9 main specifications